pendulum
Home >
M5StickC で倒立振子 Blynk でコントロール ー倒立振子への道 4ー
前回、実現できたM5StickCによる倒立振子を前進/後進/旋回動作できるようにいたしました。 https://homemadegarbage.com/bala03 倒立振子自体の制御は前回と同様にPID制御です。タイヤの回転などを加味したより安定した制御方法は現在勉強中です。いつまでかかるかな...
M5StickC で倒立振子 PID制御編 ー倒立振子への道 3ー
さて前回まででカルマン・フィルタを使用したM5StickC傾斜計を作りました。 いよいよM5StickCによる倒立振子を作っていきます。 この道シリーズではトランジスタ技術 2019年 7月号を参考に倒立振子の実現を目指しています。 [amazonjs asin="B07RS8ZTJ3" lo...
傾斜計 カルマン・フィルタ アルゴリズムの解きほぐし ー倒立振子への道 2ー
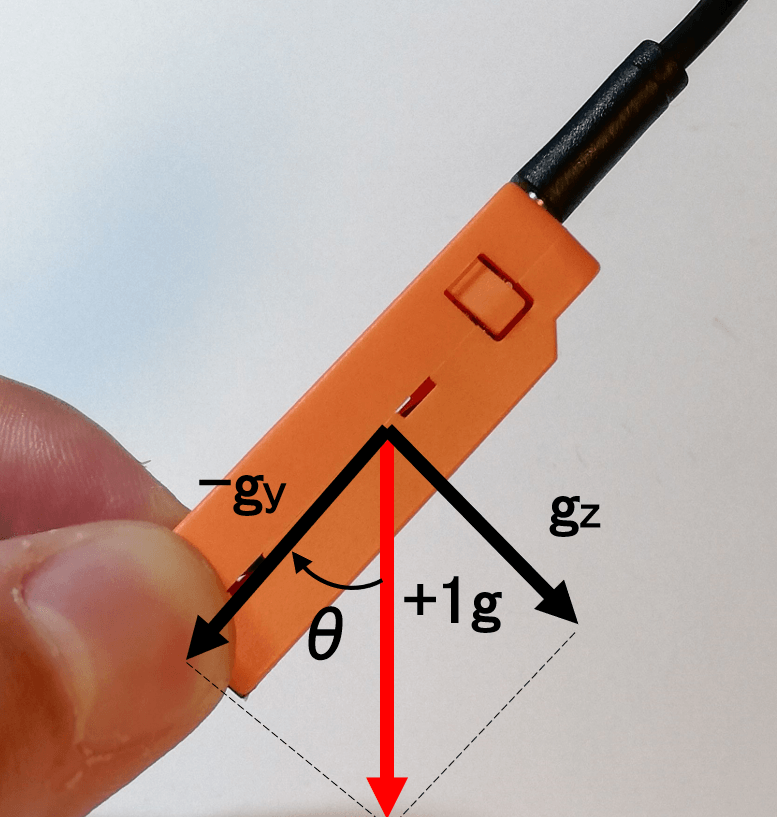
前回トラ技を参考に作ったM5stickCを用いた傾斜計ではカルマン・フィルタの効能を堪能しただけで、そのカルマン・フィルタが何をしているかはすっ飛ばして見てみぬフリをしておりました。 https://homemadegarbage.com/bala01 ここでは前回用いたコードのカルマン・フィル...
カルマン・フィルタで M5stickC 傾斜計 ー倒立振子への道 1ー
今月のトランジスタ技術が非常に興味深い内容でした。 [amazonjs asin="B07RS8ZTJ3" locale="JP" title="トランジスタ技術 2019年 07 月号"] 確率統計コンピューティング特集ということでカルマン・フィルタの歴史とカルマン倒立振子の作...