傾斜計 カルマン・フィルタ アルゴリズムの解きほぐし ー倒立振子への道 2ー
本記事にはアフィリエイト広告が含まれます。
前回トラ技を参考に作ったM5stickCを用いた傾斜計ではカルマン・フィルタの効能を堪能しただけで、そのカルマン・フィルタが何をしているかはすっ飛ばして見てみぬフリをしておりました。
ここでは前回用いたコードのカルマン・フィルタ アルゴリズムを少し解きほぐし何をしているのかをみてみたいと思います。
しかし内容がかなり難しくここでも様々な点をすっ飛ばさなくてはなりません。カルマン・フィルタが制御工学や統計学など様々な基礎学問の上に成り立っているからです。
でも気にしてはいられません。この道の目的はM5stickCを用いたオリジナルの倒立振子の実現です。今から統計や制御理論を1から学ぶのは得策ではありません。挫折するに決まっています(お父ちゃん![]() の場合)。
の場合)。
漫画家見習いが鉛筆の素材の木を植えるところから始めるわけにはいかないのですから。
目次
傾斜計コード
前回のコードを改めて記載いたします。
トラ技のソースコードInclinometer.cppをほぼ丸々参考にしています(p. 49 – 52)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 |
#include <M5StickC.h> #include <Ticker.h> int16_t accX = 0; int16_t accY = 0; int16_t accZ = 0; int16_t gyroX = 0; int16_t gyroY = 0; int16_t gyroZ = 0; //加速度センサ オフセット int16_t accXoffset = 1020; int16_t accYoffset = 450; int16_t accZoffset = 958; //ジャイロセンサ オフセット int16_t gyroXoffset = -60; int16_t gyroYoffset = -15; int16_t gyroZoffset = 370; Ticker tickerUpdate; //センサ バラつき取得用変数 int sample_num = 100; int meas_interval = 10; float theta_deg; float theta_dot_deg; float theta_mean; float theta_variance; float theta_dot_mean; float theta_dot_variance; //========================================================= //カルマン・フィルタ用変数 //========================================================= //カルマン・フィルタ処理 2.5msec(400Hz)毎に実施 float theta_update_freq = 400; //Hz float theta_update_interval = 1.0/double(theta_update_freq); //2.5msec //状態ベクトルx //[[theta(degree)], [offset of theta_dot(degree/sec)]] //状態ベクトルの予測値 float theta_data_predict[2][1]; float theta_data[2][1]; //共分散行列 float P_theta_predict[2][2]; float P_theta[2][2]; //状態方程式の"A" float A_theta[2][2] = {{1, -theta_update_interval}, {0, 1}}; //状態方程式の"B" float B_theta[2][1] = {{theta_update_interval}, {0}}; //出力方程式の"C" float C_theta[1][2] = {{1, 0}}; //========================================================= // 行列演算関数 //========================================================= //行列の和 void mat_add(float *m1, float *m2, float *sol, int row, int column) { for(int i=0; i<row; i++) { for(int j=0; j<column; j++) { sol[i*column + j] = m1[i*column + j] + m2[i*column + j]; } } return; } //行列の差 void mat_sub(float *m1, float *m2, float *sol, int row, int column){ for(int i=0; i<row; i++) { for(int j=0; j<column; j++) { sol[i*column + j] = m1[i*column + j] - m2[i*column + j]; } } return; } //行列の積 void mat_mul(float *m1, float *m2, float *sol, int row1, int column1, int row2, int column2){ for(int i=0; i<row1; i++){ for(int j=0; j<column2; j++){ sol[i*column2 + j] = 0; for(int k=0; k<column1; k++) { sol[i*column2 + j] += m1[i*column1 + k]*m2[k*column2 + j]; } } } return; } //転置行列算出 void mat_tran(float *m1, float *sol, int row_original, int column_original) { for(int i=0; i<row_original; i++) { for(int j=0; j<column_original; j++) { sol[j*row_original + i] = m1[i*column_original + j]; } } return; } //行列の定数倍算出 void mat_mul_const(float *m1,float c, float *sol, int row, int column){ for(int i=0; i<row; i++){ for(int j=0; j<column; j++){ sol[i*column + j] = c * m1[i*column + j]; } } return; } //逆行列算出 void mat_inv(float *m, float *sol, int column, int row){ //allocate memory for a temporary matrix float* temp = (float *)malloc( column*2*row*sizeof(float) ); //make the augmented matrix for(int i=0; i<column; i++) { //copy original matrix for(int j=0; j<row; j++) { temp[i*(2*row) + j] = m[i*row + j]; } //make identity matrix for(int j=row; j<row*2; j++) { if(j-row == i) { temp[i*(2*row) + j] = 1; } else { temp[i*(2*row) + j] = 0; } } } //Sweep (down) for(int i=0; i<column; i++) { //pivot selection float pivot = temp[i*(2*row) + i]; int pivot_index = i; float pivot_temp; for(int j=i; j<column;j++) { if( temp[j*(2*row)+i] > pivot ) { pivot = temp[j*(2*row) + i]; pivot_index = j; } } if(pivot_index != i) { for(int j=0; j<2*row; j++) { pivot_temp = temp[ pivot_index * (2*row) + j ]; temp[pivot_index * (2*row) + j] = temp[i*(2*row) + j]; temp[i*(2*row) + j] = pivot_temp; } } //division for(int j=0; j<2*row; j++) { temp[i*(2*row) + j] /= pivot; } //sweep for(int j=i+1; j<column; j++) { float temp2 = temp[j*(2*row) + i]; //sweep each row for(int k=0; k<row*2; k++) { temp[j*(2*row) + k] -= temp2 * temp[ i*(2*row) + k ]; } } } //Sweep (up) for(int i=0; i<column-1; i++) { for(int j=i+1; j<column; j++) { float pivot = temp[ (column-1-j)*(2*row) + (row-1-i)]; for(int k=0; k<2*row; k++) { temp[(column-1-j)*(2*row)+k] -= pivot * temp[(column-1-i)*(2*row)+k]; } } } //copy result for(int i=0; i<column; i++) { for(int j=0; j<row; j++) { sol[i*row + j] = temp[i*(2*row) + (j+row)]; } } free(temp); return; } //加速度センサから傾きデータ取得 [deg] float get_acc_data() { M5.IMU.getAccelData(&accX,&accY,&accZ); //得られたセンサ値はオフセット引いて使用 //傾斜角導出 単位はdeg theta_deg = atan( (float)(accZ - accZoffset) / (float)(-1 * accY - accYoffset) ) * 57.29578f; return theta_deg; } //加速度センサによる傾きのばらつき測定 void acc_init(){ float theta_array[sample_num]; for(int i=0; i<sample_num; i++) { theta_array[i] = get_acc_data(); delay(meas_interval); } //平均値 theta_mean = 0; for(int i=0; i<sample_num; i++) { theta_mean += theta_array[i]; } theta_mean /= sample_num; //分散 float temp; theta_variance = 0; for(int i=0; i<sample_num; i++) { temp = theta_array[i] - theta_mean; theta_variance += temp*temp; } theta_variance /= sample_num; } //x軸 角速度取得 float get_gyro_data() { M5.IMU.getGyroData(&gyroX,&gyroY,&gyroZ); //得られたセンサ値はオフセット引いて使用 theta_dot_deg = ((float) (gyroX - gyroXoffset)) * M5.IMU.gRes; return theta_dot_deg; } //ジャイロセンサばらつき測定 void gyro_init() { float theta_dot_array[sample_num]; for(int i=0;i<sample_num;i++) { theta_dot_array[i] = get_gyro_data(); delay(meas_interval); } //平均値 theta_dot_mean = 0; for(int i=0;i<sample_num;i++) { theta_dot_mean += theta_dot_array[i]; } theta_dot_mean /= sample_num; //分散 float temp; theta_dot_variance = 0; for(int i=0; i<sample_num; i++) { temp = theta_dot_array[i] - theta_dot_mean; theta_dot_variance += temp*temp; } theta_dot_variance /= sample_num; } //========================================================= //カルマン・フィルタアルゴリズム処理 //========================================================= void update_theta() { //加速度センサによる角度測定 float y = get_acc_data(); //degree //入力データ:角速度 float theta_dot_gyro = get_gyro_data(); //degree/sec //カルマン・ゲイン算出: G = P'C^T(W+CP'C^T)^-1 float P_CT[2][1] = {}; float tran_C_theta[2][1] = {}; mat_tran(C_theta[0], tran_C_theta[0], 1, 2);//C^T mat_mul(P_theta_predict[0], tran_C_theta[0], P_CT[0], 2, 2, 2, 1);//P'C^T float G_temp1[1][1] = {}; mat_mul(C_theta[0], P_CT[0], G_temp1[0], 1,2, 2,1);//CP'C^T float G_temp2 = 1.0f / (G_temp1[0][0] + theta_variance);//(W+CP'C^T)^-1 float G1[2][1] = {}; mat_mul_const(P_CT[0], G_temp2, G1[0], 2, 1);//P'C^T(W+CP'C^T)^-1 //傾斜角推定値算出: theta = theta'+G(y-Ctheta') float C_theta_theta[1][1] = {}; mat_mul(C_theta[0], theta_data_predict[0], C_theta_theta[0], 1, 2, 2, 1);//Ctheta' float delta_y = y - C_theta_theta[0][0];//y-Ctheta' float delta_theta[2][1] = {}; mat_mul_const(G1[0], delta_y, delta_theta[0], 2, 1); mat_add(theta_data_predict[0], delta_theta[0], theta_data[0], 2, 1); //共分散行列算出: P=(I-GC)P' float GC[2][2] = {}; float I2[2][2] = {{1,0},{0,1}}; mat_mul(G1[0], C_theta[0], GC[0], 2, 1, 1, 2);//GC float I2_GC[2][2] = {}; mat_sub(I2[0], GC[0], I2_GC[0], 2, 2);//I-GC mat_mul(I2_GC[0], P_theta_predict[0], P_theta[0], 2, 2, 2, 2);//(I-GC)P' //次時刻の傾斜角の予測値算出: theta'=Atheta+Bu float A_theta_theta[2][1] = {}; float B_theta_dot[2][1] = {}; mat_mul(A_theta[0], theta_data[0], A_theta_theta[0], 2, 2, 2, 1);//Atheta mat_mul_const(B_theta[0], theta_dot_gyro, B_theta_dot[0], 2, 1);//Bu mat_add(A_theta_theta[0], B_theta_dot[0], theta_data_predict[0], 2, 1);//Atheta+Bu //次時刻の共分散行列算出: P'=APA^T + BUB^T float AP[2][2] = {}; float APAT[2][2] = {}; float tran_A_theta[2][2] = {}; mat_tran(A_theta[0], tran_A_theta[0], 2, 2);//A^T mat_mul(A_theta[0], P_theta[0], AP[0], 2, 2, 2, 2);//AP mat_mul(AP[0], tran_A_theta[0], APAT[0], 2, 2, 2, 2);//APA^T float BBT[2][2]; float tran_B_theta[1][2] = {}; mat_tran(B_theta[0], tran_B_theta[0], 2, 1);//B^T mat_mul(B_theta[0], tran_B_theta[0], BBT[0], 2, 1, 1, 2);//BB^T float BUBT[2][2] = {}; mat_mul_const(BBT[0], theta_dot_variance, BUBT[0], 2, 2);//BUB^T mat_add(APAT[0], BUBT[0], P_theta_predict[0], 2, 2);//APA^T+BUB^T } void setup() { // put your setup code here, to run once: Serial.begin(115200); M5.begin(); M5.Axp.ScreenBreath(8); M5.IMU.Init(); M5.Lcd.setRotation(1); M5.Lcd.fillScreen(BLACK); //初期設定開始 LED ON pinMode(10, OUTPUT); digitalWrite(10, LOW); //センサばらつき取得 100回測って分散導出 acc_init(); gyro_init(); //カルマンフィルタの初期設定 初期姿勢は0°(直立)を想定 theta_data_predict[0][0] = 0; theta_data_predict[1][0] = theta_dot_mean; P_theta_predict[0][0] = 1; P_theta_predict[0][1] = 0; P_theta_predict[1][0] = 0; P_theta_predict[1][1] = theta_dot_variance; //Timer 2.5msec(400 Hz)ごとにカルマン・フィルタで角度導出 tickerUpdate.attach(theta_update_interval, update_theta); //初期設定終了 LED OFF digitalWrite(10, HIGH); } void loop() { /* //加速度センサによる傾斜角 Serial.print(theta_deg); Serial.print(", "); //カルマン・フィルタによる角度の推定値 Serial.println(theta_data[0][0]); */ //ジャイロセンサによるx軸角速度 Serial.print(theta_dot_deg); Serial.print(", "); //カルマン・フィルタによる角速度の推定値 Serial.println(theta_dot_deg - theta_data[1][0]); delay(50); } |
ここではカルマン・フィルタ アルゴリズム処理 update_theta()を解きほぐします。
カルマン・フィルタの概要
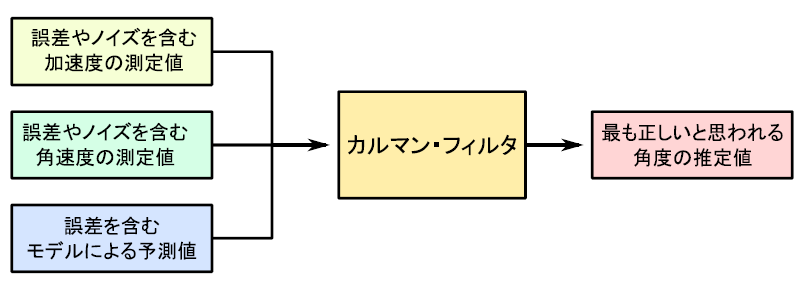
カルマン・フィルタは”センサの測定値”と”モデルから算出した予測値”を元に真値を推定するフィルタです。下は傾斜計の場合のブロック図です。
実際どういった処理を施して傾斜角の推定値を得ているのかコードより解きほぐしてみましょう。
まずはフィルタに導入する測定値と予測値についてみていきましょう。
センサによる測定値
M5stickCに内蔵されている6軸の慣性センサ(加速度、ジャイロ) SH200Q を使用して傾斜角と角速度を測ります。
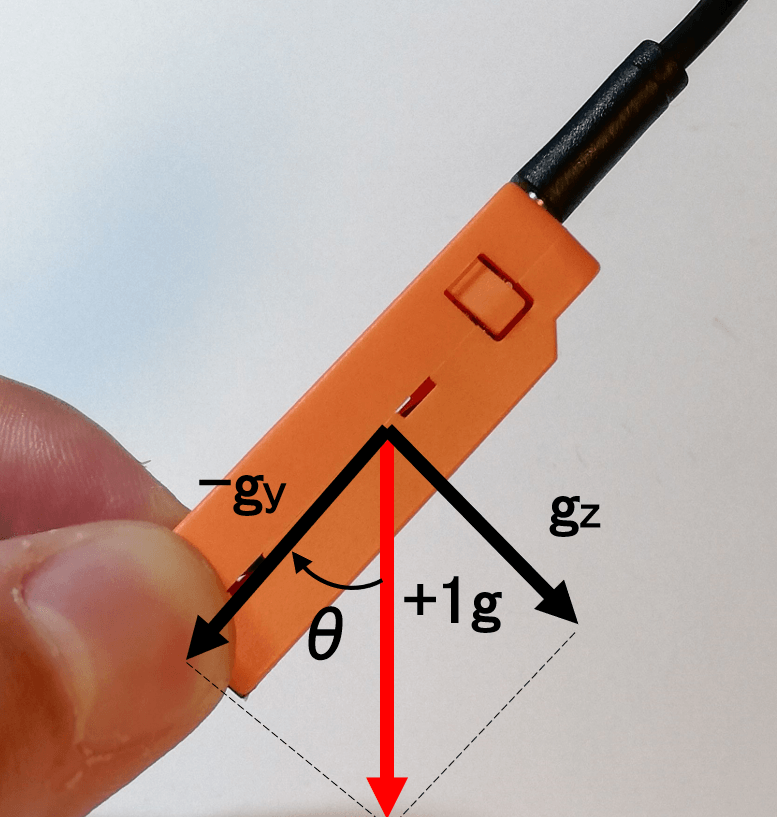
傾斜角θは加速度センサから重力加速度の傾きを検出して導出します。
角速度はジャイロセンサの値(x軸)をそのまま使用します。
数理モデルによる予測値
予測値を得るために物理現象を記述する式(数理モデル)を立てます。
傾斜角の関係式は以下の通りです。
$$θ_{k+1} = (ω_k – ω_{offset})・Δt + θ_k$$
$θ_k $は時刻kのときの傾斜角で$ω_k $は時刻kのときの角速度です。$w_{offset}$は角速度のオフセット誤差です。
時間kのときの角速度に微小時間$Δt $(コードでは2.5msec)をかけて$θ_k $を足すと$Δt $後(時間 k+1)の傾斜角$θ_{k+1}$が得られるということを示しています。
またここで簡単のため角速度(ジャイロセンサ)のオフセットは時刻によらず一定と仮定します。
$$ω_{offset}(k+1) = ω_{offset}(k)=ω_{offset}$$
ここですっ飛ばしブチかましますが、現代制御理論では数理モデルを行列で表現する習わしがあるそうです。
状態方程式
物理状態の移り変わりを示すのが状態方程式です。上記2式より以下で表せます。
$$\left( \begin{array}{c} θ_{k+1}\\ ω_{offset} \end{array} \right)=\left( \begin{array}{cc} 1&-Δt\\0&1 \end{array} \right)\left( \begin{array}{c} θ_{k}\\ ω_{offset} \end{array} \right)+\left( \begin{array}{c} Δt\\ 0 \end{array} \right)ω_k$$
一般式では以下のように書きます。
$$x_{k+1}=A・x_k+B・u_k$$
ここでの物理状態$x$ ($θ_k$と$ω_{offset}$)は行列Aをかけて2項目の入力$ω_k$(角速度)に関する値を足すと次の状態があられることを示しています。
出力方程式
物理状態で実際に観測できる状態(値)を示す行列式です。
$$θ_k=\left( \begin{array}{cc} 1&0\end{array} \right)\left( \begin{array}{c} θ_{k}\\ ω_{offset} \end{array} \right)$$
$θ_{k}$だけがセンサから直接得られることを示しています。$ω_{offset}$だけを得ることはできませんのでね。
一般式は以下で書きます。
$$y_k=C・x_k$$
以上で数理モデルが用意できました。また行列A, B, Cは時間依存のない定数でした。
カルマン・フィルタ アルゴリズム
やっとコードのカルマン・フィルタ アルゴリズムupdate_theta()が何をやっているかをみてみます。かなりすっ飛ばします。とにかくここではコード上でどんな処理をしているかをみるのが目的です。よく理解できないし。。ここでは丸飲みします。
update_theta()は以下の5つの処理を実行しています。
- カルマン・ゲイン$G_k$の算出
- 現時点kの推定値$\hat x_k$の算出
- 現時点kの共分散行列$P_k$の算出
- 次時刻k+1の予測値$\tilde x_{k+1}$の算出
- 次時刻k+1の共分散行列$P’_{k+1} $の算出
1. カルマン・ゲイン算出
カルマン・ゲイン$G_k$とはモデルによる予測値$\tilde x_k$とセンサによる測定値$y_k$を混ぜ合わせて推定値$\hat x_k$を求める際の重みづけ配分比を意味します。
そして詳細は分かりませんが$G_k$は以下の式で得られます。
$$G_k=P’_k C^T(W + C P’_k C^T)^{-1}$$
$P’_k$:前時刻に算出された共分散行列(5. で算出)
$C^T$:出力方程式の係数行列C = $\left( \begin{array}{cc} 1&0\end{array} \right)$の転置。つまり$\left( \begin{array}{c} 1\\0\end{array} \right)$
$W$:観測雑音の程度を表す量。つまり加速度センサによる角度の分散(theta_variance)
2. 推定値算出
前時刻に算出された予測値(4. で算出)$\tilde x_{k}$と測定値$y_k = θ_{k}$からカルマン・ゲイン$G_k$を絡めて推定値$\hat x_k$を求めます。
$$\hat x_k=\tilde x_k+G_k(y_k – C \tilde x_k)$$
3. 共分散行列算出
共分散行列とはデータをxとyとすると$\left( \begin{array}{cc} {σ_x}^2 & {σ_{xy}}^2\\ {σ_{xy}}^2 & {σ_y}^2\end{array} \right)$で表されます。
要するにデータをxとyの変動の相関を表します。
データxとyに相関がない場合は分散$ {σ_{xy}}^2 = 0$となります。
物理状態$θ_k$の共分散行列$P_k$は以下で表されます。例によってなんでかは知りません。
$$P_k = (I_2 – G_k C) P’_k$$
$I_2$:2行2列の単位行列$\left( \begin{array}{cc} 1&0\\0&1\end{array} \right)$
$G_k$:カルマン・ゲイン
$C$:出力方程式の係数行列C = $\left( \begin{array}{cc} 1&0\end{array} \right)$
$P’_k$:前時刻に算出された共分散行列(5. で算出)
4. 次時刻の予測値算出
モデルを用いて次時刻k+1の傾斜角予測値$\tilde x_{k+1}$を算出します。
$$\tilde x_{k+1} = A \hat x_k + B \bar u_k$$
$A$:状態方程式の係数行列$\left( \begin{array}{cc} 1&-Δt\\0&1 \end{array} \right)$
$B$:状態方程式の係数行列$\left( \begin{array}{c} Δt\\0\end{array} \right)$
$ \hat x_k$:現時刻の傾斜角推定値(2. で算出)
$ \bar u_k$:入力(角速度)の平均。ここでは現時刻の角速度測定値$ω_k$で近似。
5. 次時刻の共分散行列算出
これもよくわかりませんが次時刻k+1の共分散行列は以下で得られます。
$$P’_{k+1} = A P_k A^T + B U B^T$$
$P_k$:現時刻に算出された共分散行列(3. で算出)
$U$:入力雑音の程度を表す量。つまり角速度の分散(theta_dot_variance)
カルマン・フィルタの初期設定
カルマン・フィルタの処理は前回算出した予測値と共分散行列を用いて推定を行います。常に前のデータを必要とするので最初に起動(k=0)する際には手動で初期値を指定する必要があります。
アルゴリズムの4. と5. で算出する次時刻の予測値が時刻0の時点ではないのであらかじめそれらしい値を決める必要があるということです。
コードでは初期の傾斜は直立であると条件付けして初期値を与えています。
状態予測値の初期設定
$\tilde x_0 = \left( \begin{array}{c} θ\\ ω_{offset} \end{array} \right) = \left( \begin{array}{c} 0\\ \bar ω \end{array} \right)$
直立を仮定しているため $θ = 0$、 動かしていないと仮定して$ω_{offset}$をジャイロの平均値としています。
共分散行列の初期設定
$P’_{0} =\left( \begin{array}{cc} {σ_θ}^2&0\\0&{σ_{ω_{offset}}}^2 \end{array} \right) =\left( \begin{array}{cc} 1&0\\0&{σ_ω}^2 \end{array} \right)$
角度のばらつきは1°程度と想定し、$ω_{offset}$のばらつきはジャイロの測定値のばらつきとしています。傾斜角と$ω_{offset}$に相関はないので対角の値は0です。
初期値の値は多少ずれがあっても時刻が進み測定データが増えると推定値は真値付近に収束するようです。
おわりに
傾斜計コードで使用したカルマン・フィルタ アルゴリズムの処理内容を追いかけました。
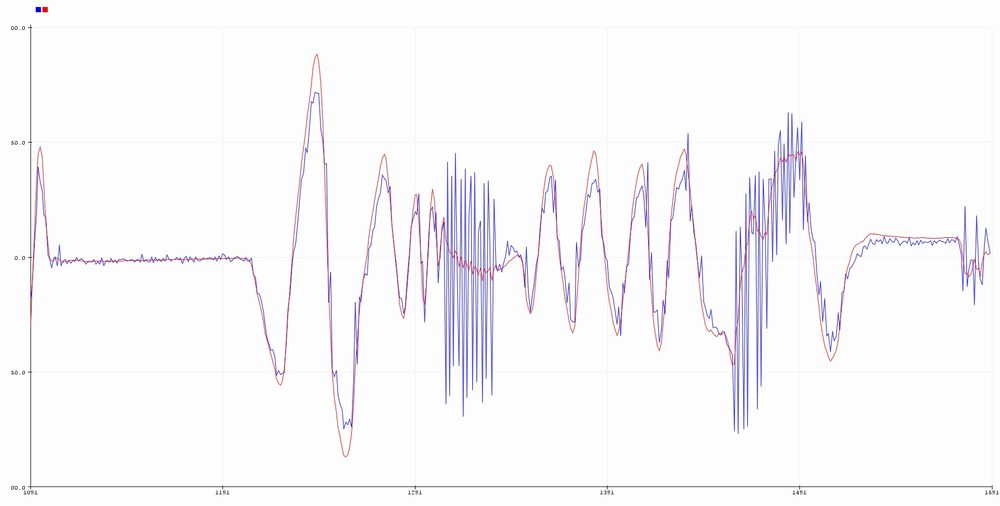
数式などは分からないことが多々ありますが、確かにその処理をしていい感じの結果を得ているのです。
とにかくカルマン・フィルタ アルゴリズムを飲み込んで数理モデル方程式を立てて初期値の設定をそれらしく実施すればよいとのことなので応用が利くことでしょう。
さて次は倒立振子に向けて動きたいと思います。
 お父ちゃん
2019.6.23
お父ちゃん
2019.6.23