月: 2019年6月
傾斜計 カルマン・フィルタ アルゴリズムの解きほぐし ー倒立振子への道 2ー
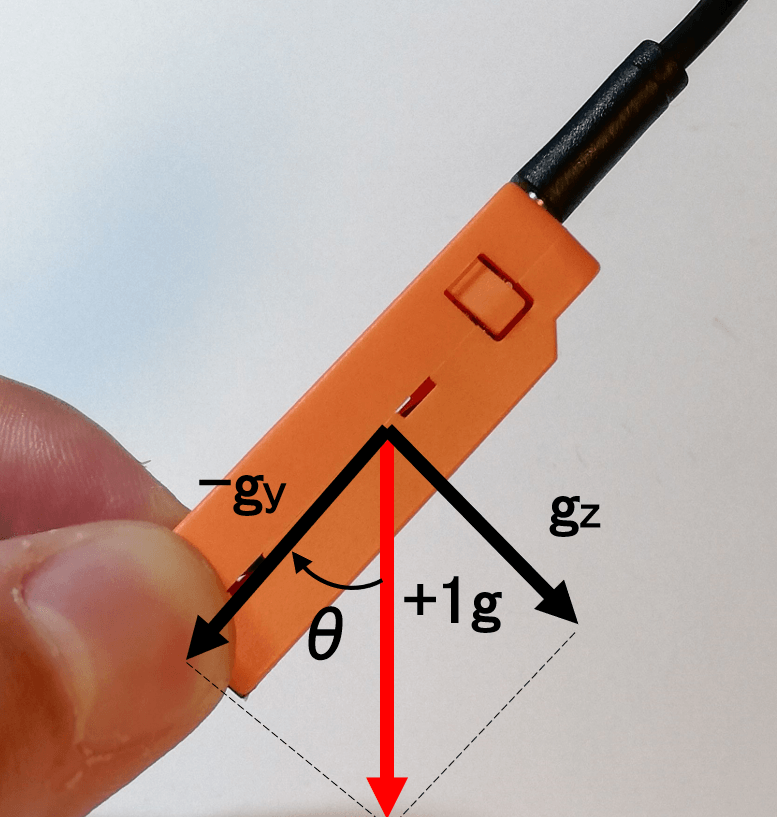
前回トラ技を参考に作ったM5stickCを用いた傾斜計ではカルマン・フィルタの効能を堪能しただけで、そのカルマン・フィルタが何をしているかはすっ飛ばして見てみぬフリをしておりました。 https://homemadegarbage.com/bala01 ここでは前回用いたコードのカルマン・フィル...
日射量データベースから太陽光発電量を算出 ーベランダ太陽光発電所への道6ー
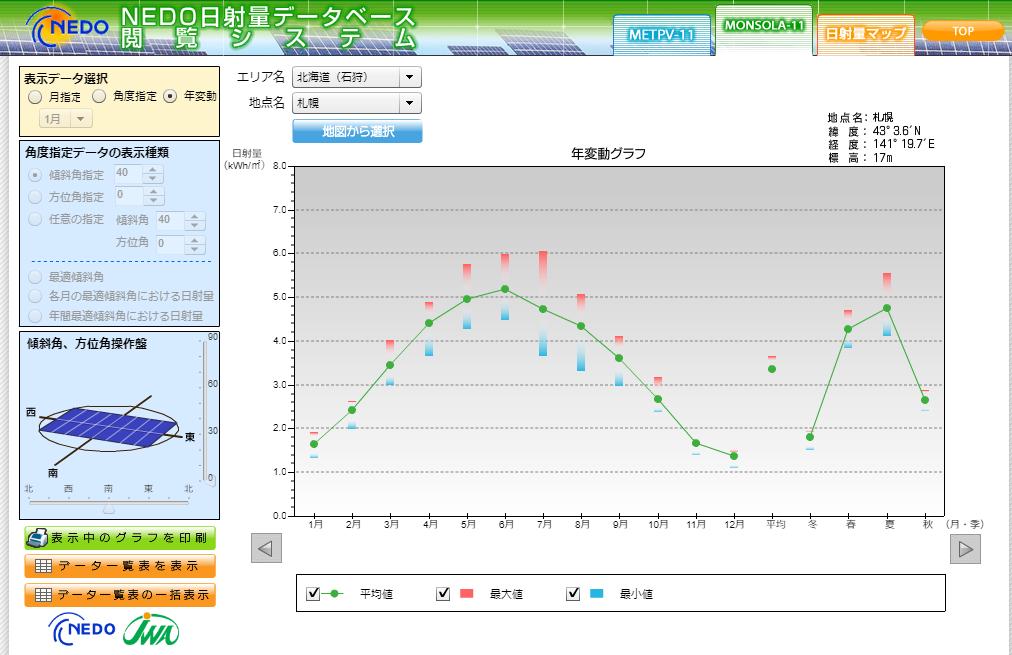
我が家のベランダは西向きであまり日照時間が長くなく、それに伴い発電も主に午前中に実施されることがわかっています(6:00~11:00)。 発電したい電力量がわかっていて、設置場所の日射量がわかっていれば、どのくらいのサイズのソーラーパネルを購入すればいいかが前もって見積もれます。 各地の日射...
カルマン・フィルタで M5stickC 傾斜計 ー倒立振子への道 1ー
今月のトランジスタ技術が非常に興味深い内容でした。 [amazonjs asin="B07RS8ZTJ3" locale="JP" title="トランジスタ技術 2019年 07 月号"] 確率統計コンピューティング特集ということでカルマン・フィルタの歴史とカルマン倒立振子の作...
M5StickC でスマートな電池を作製 M5Stick-Cell
ついに購入しました!M5StickCを。 M5StickCは大人気のM5Stackの小型版です。M5Stackは持っていなかったのですがM5StickCのカワイイ色やサイズそして何と言っても2千円以下の家計に優しい価格にやられて速攻購入した次第です。 ここではM5StickCを用いて製作した実に...
SPRESENSE のマルチコアプログラミングで バーサライタ
ついにSPRESENSE にArduino IDEでのマルチコアプログラミング環境が誕生しました。 [amazonjs asin="B07H2CG1HP" locale="JP" title="SONY SPRESENSE メインボード CXD5602PWBMAIN1"] 前回S...
太陽光発電でタイムラプス撮影 ーベランダ太陽光発電所への道5ー
いよいよ太陽光発電を本格運用します。ここではラズパイカメラをつないでタイムラプス撮影を実施したのでご報告します。 構成 ソーラーパネルと鉛蓄電池をチャージコントローラに接続します。負荷としてラズパイカメラをつなげました。 部品 ソーラー充電コント...
E32-SolarCharger の PWM制御 ーベランダ太陽光発電所への道4ー
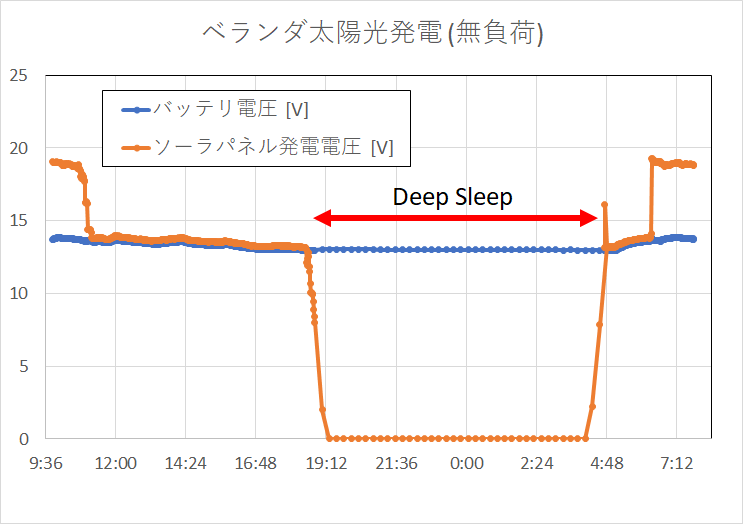
さてこれまでソーラー充電コントローラの基本機能を学んできましたが、いよいよ発電開始!です。 実際にソーラーパネルとバッテリをつないで動かしていきましょう。 構成 ソーラーパネルと鉛蓄電池をコントローラに接続します。今回は負荷はつなげていません。 コントローラと蓄電池の+側...