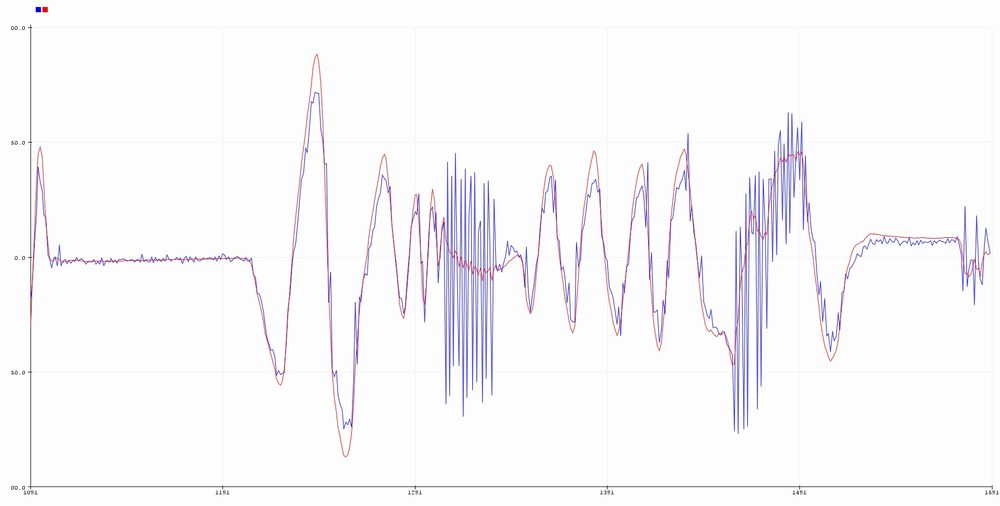
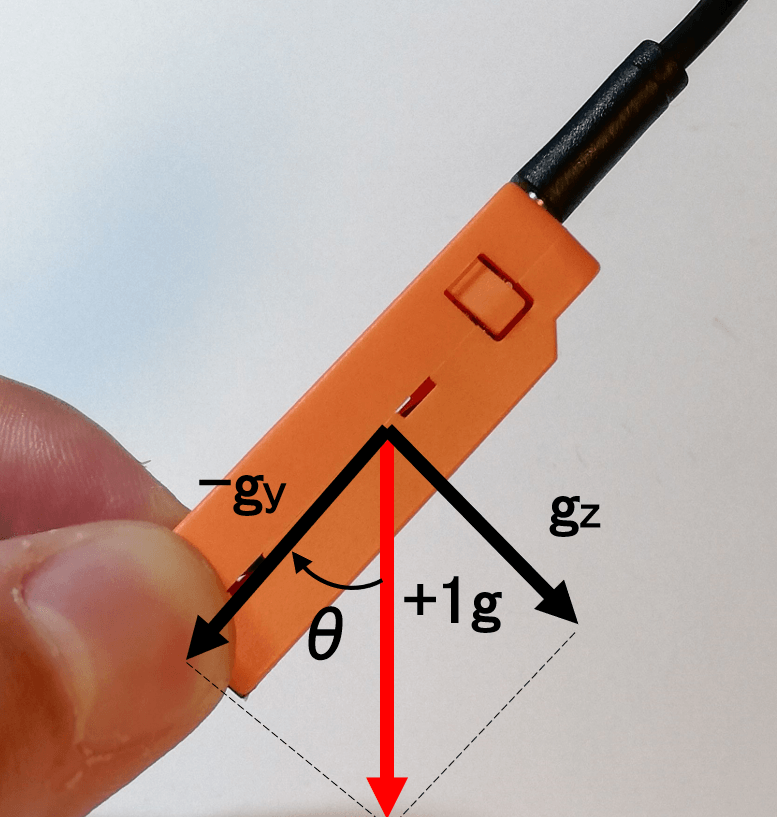
カルマンフィルタ
Seeed XIAO BLE nRF52840 Sense で1軸 姿勢制御モジュール 製作
先日はSeeed XIAO BLE nRF52840 Sense の味見をいたしました。 https://homemadegarbage.com/xiao-sense01 [bc url="https://www.seeedstudio.com/Seeed-XIAO-BLE-Sense-nRF5...
Seeed XIAO BLE nRF52840 Sense を使ってみた
Seeed XIAO BLE nRF52840 Sense を購入し味見してみましたので報告いたします。 [bc url="https://www.seeedstudio.com/Seeed-XIAO-BLE-Sense-nRF52840-p-5253.html"] ...
1軸 姿勢制御モジュール がやっと立った ーリアクションホイールへの道7ー
さて、前回の1軸 姿勢制御モジュール SHISEIGYO-1 (シセーギョーワン) 倒立に向けた下準備から随分日が経ちました。 実はずーーーーっと倒立させるべく試行錯誤しておりました。 この度無事になんとか倒立させることができましたのでご報告いたします。 倒立した...
1軸 姿勢制御モジュール の倒立に向けた準備 ーリアクションホイールへの道6ー
前回は1軸姿勢制御モジュールの筐体を製作し、簡単な動作確認を実施いたしました。 今回は姿勢制御モジュールの倒立実現に向けていくつか検討、改修を施したので 報告いたします。 エンコーダ導入 前回の動作確認段階でP制御では倒立しそうもないことは、体感的に理解できまし...
1軸 姿勢制御モジュール の筐体製作 ーリアクションホイールへの道5ー
前回はM5Stack ATOM Matrixと内蔵の慣性センサMPU6886でモータ制御するところまで確認いたしました。 ここでは1軸姿勢制御モジュールの筐体を作りこんで 簡単に動作確認を実施いたしました。 筐体製作 1軸姿勢制御モジュールの筐体を製作します。 筐体は3Dプリ...
ATOM Matrix の慣性センサでモータ制御 ーリアクションホイールへの道4ー
前回はM5Stack ATOM Matrixでカルマン・フィルタを用いた傾斜計を製作しました。 ここでは検出した姿勢角でブラシレスモータを制御して1軸の姿勢制御モジュールの実現への足掛かりにしたいと思います。 構成 ATOM MatrixのG26ピンで20kH...
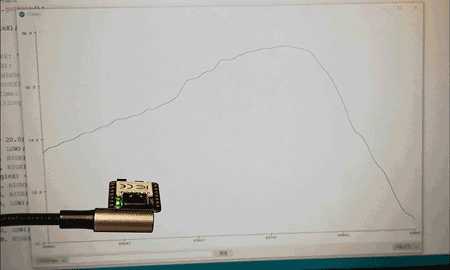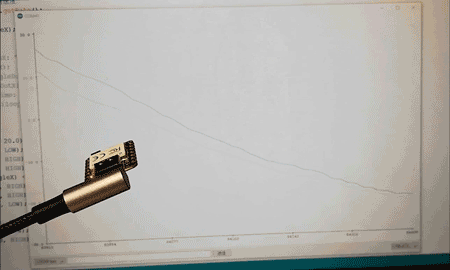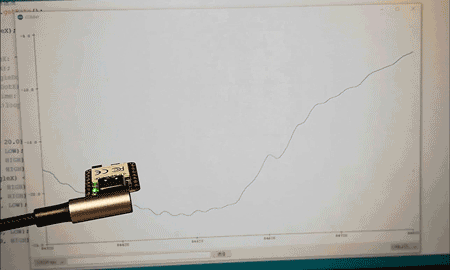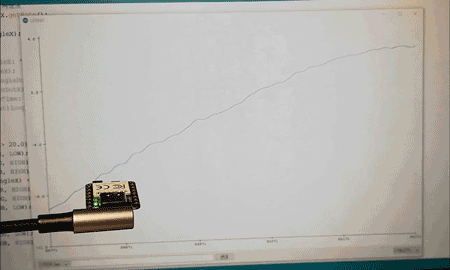
カルマン・フィルタで ATOM Matrix 傾斜計 ーリアクションホイールへの道3ー
これまではフライホイール付きブラシレスモータの制御について学習してまいりました。 ここでは1軸の姿勢制御モジュールの実現に向けて、カルマン・フィルタを用いて M5Stack ATOM Matrix に搭載された6軸慣性センサ MPU6886 で姿勢角を導出します。 6軸セン...
M5StickC で倒立振子 Blynk でコントロール ー倒立振子への道 4ー
前回、実現できたM5StickCによる倒立振子を前進/後進/旋回動作できるようにいたしました。 https://homemadegarbage.com/bala03 倒立振子自体の制御は前回と同様にPID制御です。タイヤの回転などを加味したより安定した制御方法は現在勉強中です。いつまでかかるかな...
M5StickC で倒立振子 PID制御編 ー倒立振子への道 3ー
さて前回まででカルマン・フィルタを使用したM5StickC傾斜計を作りました。 いよいよM5StickCによる倒立振子を作っていきます。 この道シリーズではトランジスタ技術 2019年 7月号を参考に倒立振子の実現を目指しています。 [amazonjs asin="B07RS8ZTJ3" lo...
傾斜計 カルマン・フィルタ アルゴリズムの解きほぐし ー倒立振子への道 2ー
前回トラ技を参考に作ったM5stickCを用いた傾斜計ではカルマン・フィルタの効能を堪能しただけで、そのカルマン・フィルタが何をしているかはすっ飛ばして見てみぬフリをしておりました。 https://homemadegarbage.com/bala01 ここでは前回用いたコードのカルマン・フィル...
カルマン・フィルタで M5stickC 傾斜計 ー倒立振子への道 1ー
今月のトランジスタ技術が非常に興味深い内容でした。 [amazonjs asin="B07RS8ZTJ3" locale="JP" title="トランジスタ技術 2019年 07 月号"] 確率統計コンピューティング特集ということでカルマン・フィルタの歴史とカルマン倒立振子の作...