センサレス姿勢制御モジュール完成 ーリアクションホイールへの道54ー
本記事にはアフィリエイト広告が含まれます。
先日は電流センサを用いて回転速度を推定するDCモータのセンサレス制御について学習しました。
ここではこのセンサレス回転速度制御を姿勢制御モジュールに応用してみます。
目次
SHISEIGYO-1 DC 改造
1軸姿勢制御モジュール SHISEIGYO-1 DC をモータ電流をセンシングできるように改造して、回転速度を推定しての倒立を目指します。
電流センサは以下を使用して、モータ配線間に挿入します。
コントローラはセンサレス回転制御の検討時と同様にATOMS3を採用しました。
回転速度を推定するので磁気エンコーダは除去しました。
今回使用した基板はモータドライバ (DRV8835)を裏面に実装する古いものを使用しました。
回転速度推定
1軸姿勢制御モジュール SHISEIGYO-1 DC は以下のようにモジュールの姿勢角($θ_b$) とその角速度($\dotθ_b$) とモータの回転速度($\omega$) からモータに入力するべき電圧 (実際にはモータドライバに印可するPWM信号のデューティ比)を導出しています。
$K_p$、$K_d$、$K_w$は調整パラデータ
$$V = K_p・θ_b+K_d・\dotθ_b+K_w・\omega (1)$$
ここではモータの回転速度($\omega$) を磁気エンコーダによるものから電流センサによる推定値に変更します。
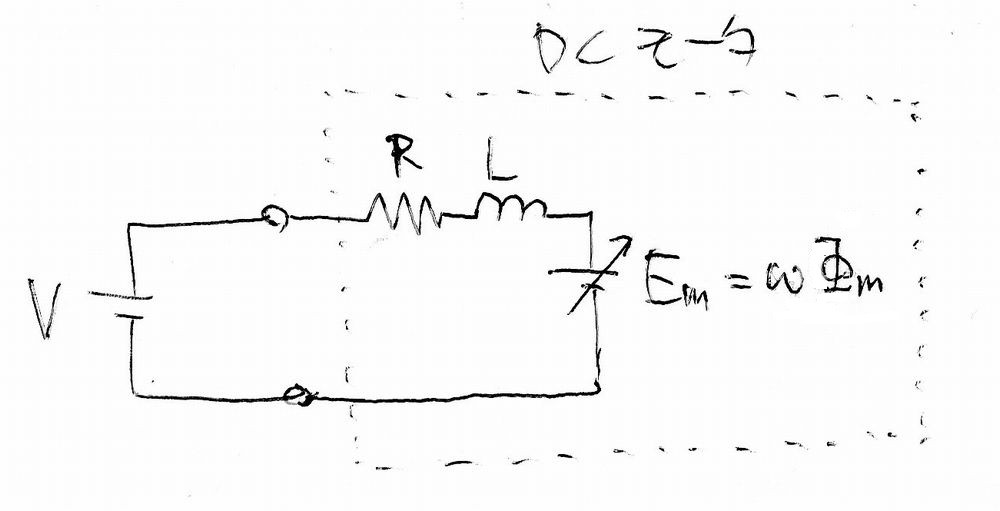
モータは以下のようにモデル化できます。$E_m$は誘起電圧
上のモデルより回転速度($\omega$)は以下で導出できます。
$$\omega=\frac{V-(R+sL)I}{\Phi_m}\fallingdotseq\frac{V-RI}{\Phi_m} (2)$$
インダクタンスの微分項は無視します。倒立時の応答はそれなりに早いので無視できない可能性ありますが簡単のために省略します!
Vは式(1)で算出された値、Iは電流センサで検出した値を用います。
モータの抵抗$R$と磁束密度$\Phi_m$は前回測定した値を使用します。
式(2)で得た推定回転速度を式(1)の$\omega$にフィードバックして姿勢制御回転をさせます。
参考文献
倒立動作
電流センサで回転速度を推定して倒立動作の検証を実施しました。
問題なく倒立動作が実現されました。
この変更に際して式(1)の$K_p$、$K_d$、$K_w$は再調整しました。
おわりに
ここでは電流を検知して回転速度を推定し、磁気エンコーダなしでの姿勢制御モジュールの倒立動作を実現しました。
センサレス姿勢制御モジュールの爆誕です!
(まぁ電流センサ使ってるんだけど。。)
DCモータはフライホイールと磁気エンコーダ用の円盤磁石を取り付けるためにダブルシャフトモータを使っておりました。
この度 磁気エンコーダの除去が実現されたので、普通のモータでも姿勢制御できそうです。
また、電流センシング機能付きモータドライバを採用することで更にコンパクトなシステムが実現できるかもしれません。