SHISEIGYO-1 Walker Jr. 差動駆動型リンク機構で歩行
本記事にはアフィリエイト広告が含まれます。
前回はSHISEIGYO-1 Walker Jr. の足に平行リンク機構を採用し、ヒザのある歩行を実現いたしました。
ここでは差動駆動型リンク機構を試しましたので報告いたします。
目次
差動駆動型リンク機構
差動駆動型リンク機構を用いれば、モータを上部に2個配置するのみでヒザ上げや足の前後移動が可能になります。
差動駆動型リンク機構
はぁーこいつはゴキゲンだ
上部にサーボ2つでいけるんだわ。#Fusion360 pic.twitter.com/uSfx70GP28— HomeMadeGarbage (@H0meMadeGarbage) September 27, 2022
早速 Fusin360上でSHISEIGYO-1 Walker Jr. の足に差動駆動型リンク機構を取り入れてみました。
差動駆動型リンク機構
実に良い pic.twitter.com/BR3xXqX0Lk— HomeMadeGarbage (@H0meMadeGarbage) September 28, 2022
非常にいい感じです。
足製作
CAD設計した足を3Dプリントして組み立てます。
片足完成。うまくいった。
期待は高まった pic.twitter.com/PB29nhXBR4
— HomeMadeGarbage (@H0meMadeGarbage) September 29, 2022
もう片方も完成。遂に憧れの屈伸運動ができるようになりました。
屈伸ができるようになった。
ヒザと言えば屈伸 pic.twitter.com/ywBYYMlwsR— HomeMadeGarbage (@H0meMadeGarbage) September 29, 2022
参考
- ROBO-ONEにチャレンジ! 二足歩行ロボット自作ガイド
足動作検証
差動駆動型リンク機構の足が完成しましたので、歩行に向けて足踏み動作を確認しました。
回転なおった pic.twitter.com/olSx3SoNGP
— HomeMadeGarbage (@H0meMadeGarbage) September 29, 2022
機構の関節の締め付けが甘く足踏みのたびに回転してしまいましたが、調整で改善しました。
足踏み動作も実現されましたので いよいよ歩行に挑戦です。
逆運動学
差動駆動型リンク機構によって足先の上下、前後移動が可能になりました。
これまではサーボモータの角度を直接指定して動作させてきましたが、ここからは足先の座標を指定して逆運動学でサーボ角度を算出して制御します。
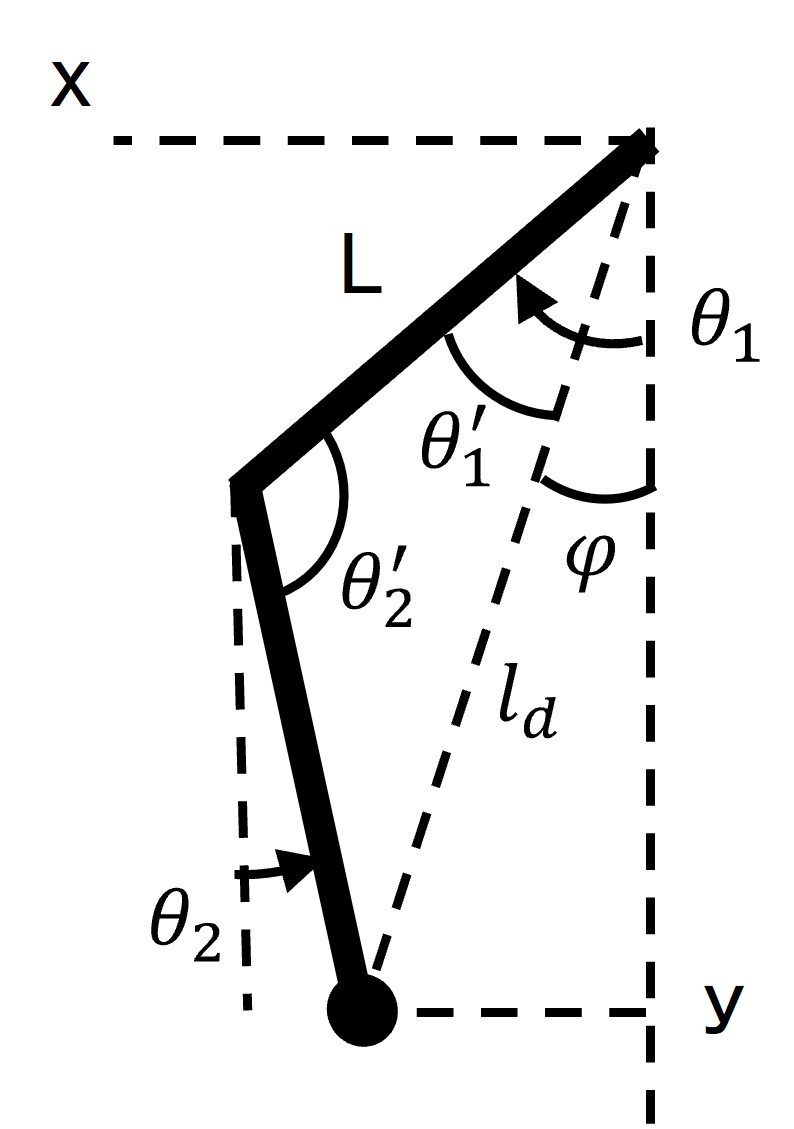
座標は以下のように定義しました。
逆運動学 算出
前方サーボの角度$θ_1$は余弦定理を用いて導出します。ちなみに$L$は大腿、下腿の長さ(36mm)。
$L^2 = L^2 + {l_d}^2 – 2{L}{l_d}\cos{θ_1}’ $
${θ_1}’ = \cos^{-1} \left(\frac{l_d}{2{L}} \right)$
$$θ_1 = φ + {θ_1}’ = φ +\cos^{-1} \left(\frac{l_d}{2{L}} \right) $$
$$ 但し、φ = \tan^{-1} \left(\frac{x}{y} \right)$$
$$ l_d = \sqrt{x^2 + y^2}$$
後方サーボの角度$θ_2$も余弦定理を用いて導出します。
${l_d}^2 = L^2 + L^2 – 2{L}{L}\cos{θ_2}’ = 2L^2 – 2L^2\cos{θ_2}’$
${θ_2}’ = \cos^{-1} \left(\frac{2L^2-{l_d}^2}{2{L}^2} \right)$
$$θ_2 =\pi-θ_1-{θ_2}’ = \pi-θ_1-\cos^{-1} \left(\frac{2L^2-{l_d}^2}{2{L}^2} \right)$$
以上より、足先の座標(x, y)からサーボモータの角度を導出できるようになりました。
動作
まずは逆運動学で足の高さを指定して、屈伸と足踏み動作を確認しました。
なめらかで非常に良い動きです。サーボの駆動音も低減されました。
歩行
いよいよ歩行です。
SHISEIGYO-2 Walkerで検証した歩行メソッドを適応させます。
歩行検討
片足を上げて前方に下げると同時に他方を後ろに下げて前進する人間っぽい歩行を目指した。ホイールをギリギリまで調整してもっと大股にしたい pic.twitter.com/ARfKq5G1C9
— HomeMadeGarbage (@H0meMadeGarbage) January 17, 2022
ヒザによる足上げを伴う歩行が遂に実現されました。
歩みを徐々に速くしてみた。
おわりに
ここではSHISEIGYO-1 Walker Jr. の足に差動駆動型リンク機構を採用し、さらに足を逆運動学で制御することでの歩行動作を確認いたしました。
差動駆動型リンク機構によって片足サーボ2個のみで足先の上下前後動作ができ、
逆運動学によってスムーズな移動が実現されました。
その半面、機構が複雑になったことにより足のブレも大きくなり若干バランスが悪化しフライホイールの調整は難しかったです。
今後の課題といたしましては差動駆動型リンク機構による足の製作の精度向上が挙げられます。
SHISEIGYO-1 Walker Jr. は1週間ほどで大きく進化しましたので、引き続き取り組んでいきます!