SHISEIGYO-2 Walker の歩行を再検討1
本記事にはアフィリエイト広告が含まれます。
以前製作したリアクションホイールを用いた2足歩行ロボットSHISEIGYO-2 Walker の歩行について再度検討したいと思います。
目次
SHISEIGYO-2 Walker
バランスを2個のリアクションホイールでとって、二足歩行するロボットです。
片足を2個、合計4個のサーボモータで足を動かします。
これまでSHISEIGYO-2 Walkerの歩行は直接サーボの角度を指定して操作しておりました。
今後より精度よく足を操作するために逆運動学による制御を検討しました。
逆運動学
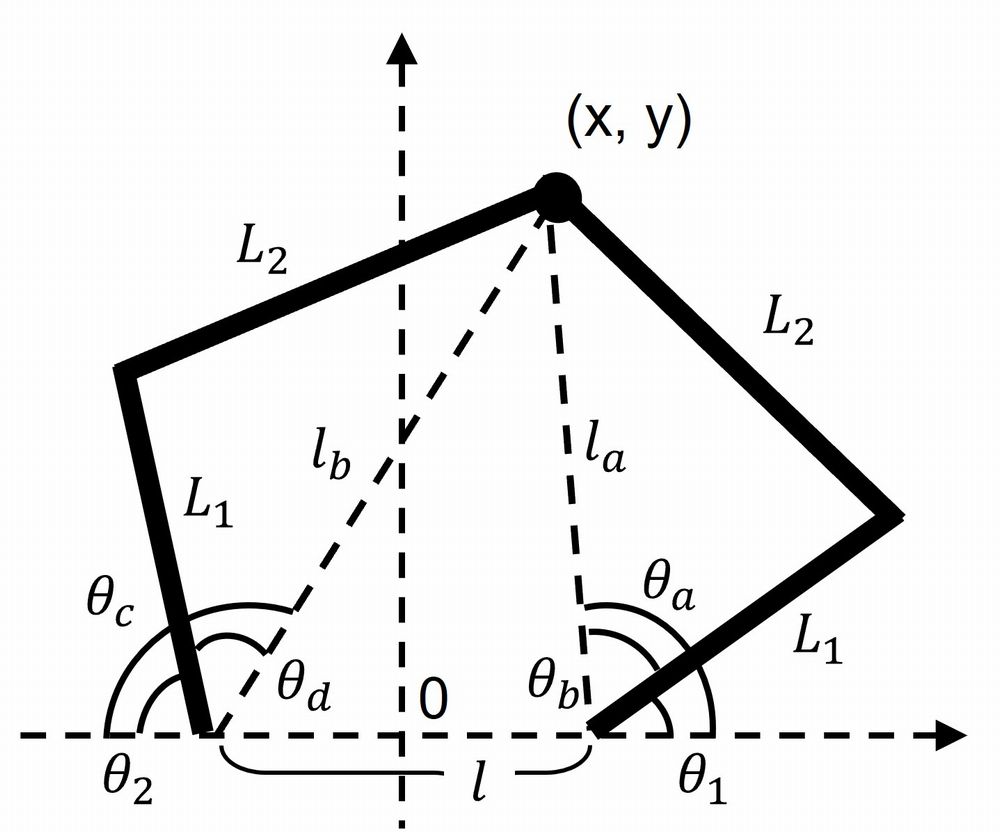
足の座標 (x, y) からサーボの角度 ($θ_1$, $θ_2$)を導出します。
片足の座標は以下で定義しました。
サーボのアームの長さは$L_1$、下肢の長さは$L_2$、サーボの軸間の長さを$l$とします。
各サーボの角度$θ_1$, $θ_2$は以下で導出されます。
$$θ_1=θ_a-θ_b$$
$$θ_2=θ_c-θ_d$$
$θ_a$, $θ_b$, $θ_c$, $θ_d$は三角比や余弦定理より以下で導出できます。
$θ_a = \tan^{-1} \left(\frac{y}{x-l/2} \right)$
${L_2}^2 = {L_1}^2 + {l_a}^2 – 2{L_1}{l_a}\cos{θ_b} $
$θ_b=\cos^{-1} \left(\frac{ {L_1}^2+ {l_a}^2- {L_2}^2}{2{L_1}{l_a}} \right)$
$π-θ_c = \tan^{-1} \left(\frac{y}{x+l/2} \right)$
$θ_c =π- \tan^{-1} \left(\frac{y}{x+l/2} \right)$
${L_2}^2 = {L_1}^2 + {l_b}^2 – 2{L_1}{l_b}\cos{θ_d} $
$θ_d=\cos^{-1} \left(\frac{ {L_1}^2+ {l_b}^2- {L_2}^2}{2{L_1}{l_b}} \right)$
よってサーボの角度$θ_1$, $θ_2$は足先の座標 (x, y)より以下で導出できる。
$$θ_1=\tan^{-1} \left(\frac{y}{x-l/2} \right)-\cos^{-1} \left(\frac{ {L_1}^2+ {l_a}^2- {L_2}^2}{2{L_1}{l_a}} \right)$$
$$θ_2=π- \tan^{-1} \left(\frac{y}{x+l/2} \right)-\cos^{-1} \left(\frac{ {L_1}^2+ {l_b}^2- {L_2}^2}{2{L_1}{l_b}} \right)$$
$$ 但し、l_a = \sqrt{\left(x-l/2\right)^2 + y^2}$$
$$ l_b = \sqrt{\left(x+l/2\right)^2 + y^2}$$
動作
導出した逆運動学の式に基づいて、片足の座標を指定して動かしてみました。
SHISEIGYO-2 Walker を逆運動学で足制御 pic.twitter.com/1OFP5EKfEp
— HomeMadeGarbage (@H0meMadeGarbage) January 13, 2022
スマホアプリBlynkで座標をジョイスティックで指定してBLEでSHISEIGYO-2 Walkerのコントローラ (ESP32)に送っています。
おわりに
ここでは2足歩行ロボット SHISEIGYO-2 Walkerの足を逆運動学での制御を検討しました。
制御関数が導出できましたので、次回は歩行座標を検討して歩かせてみたいと思います。