逆運動学 で制御 ーロボットアーム自作への道2ー
本記事にはアフィリエイト広告が含まれます。
さて今回は前回作ったロボットアームを本格的に動かしていきたいと思います。
以下の書籍で逆運動学なるものを知りましたので、その逆運動学でロボットアームを制御します。
ここではアームにペンをつけて文字を書かせてみます。
目次
逆運動学とは
前回は各サーボモータの角度を指定して、ロボットアームの姿勢を制御していました。つまり各サーボの角度でアーム先端の座標(x, y, z)が決まります。これを順運動学(Forward Kinematics)といいます。
逆運動学(Inverse Kinematics)とは、まさに逆でロボットアーム先端の座標(x, y, z)を指定して、各サーボの角度を算出する手法です。IKなどと言われているようです。
逆運動学によるサーボ角度算出
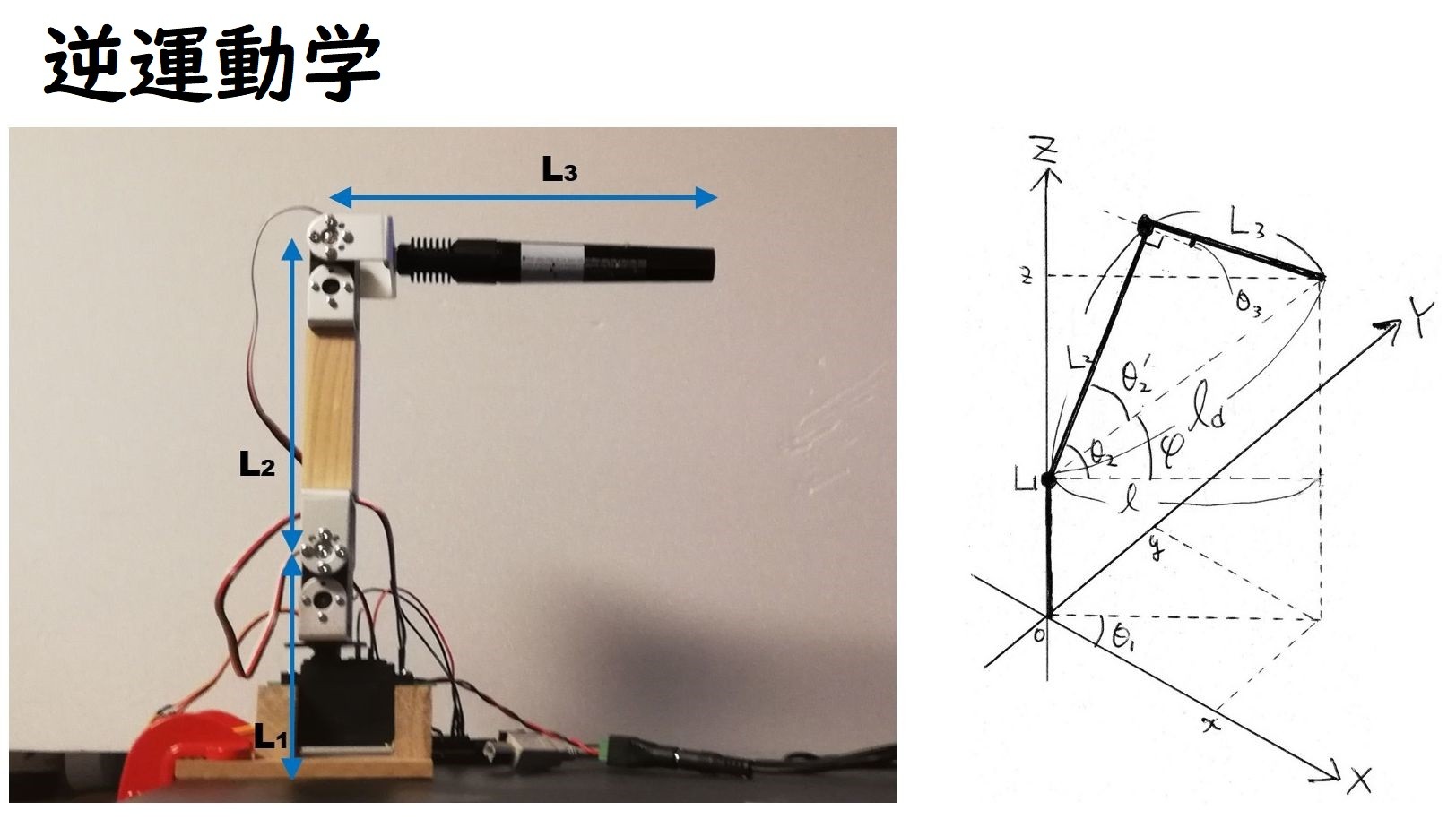
前回作ったロボットアームにマジックペンをつけて、ペン先の座標を指定して文字を書くことを目指します。
各アームの長さは以下の通りです。
$L_1 = 92$ mm
$L_2 = 137$ mm
$L_3 = 165$ mm
それでは算出していきましょう!
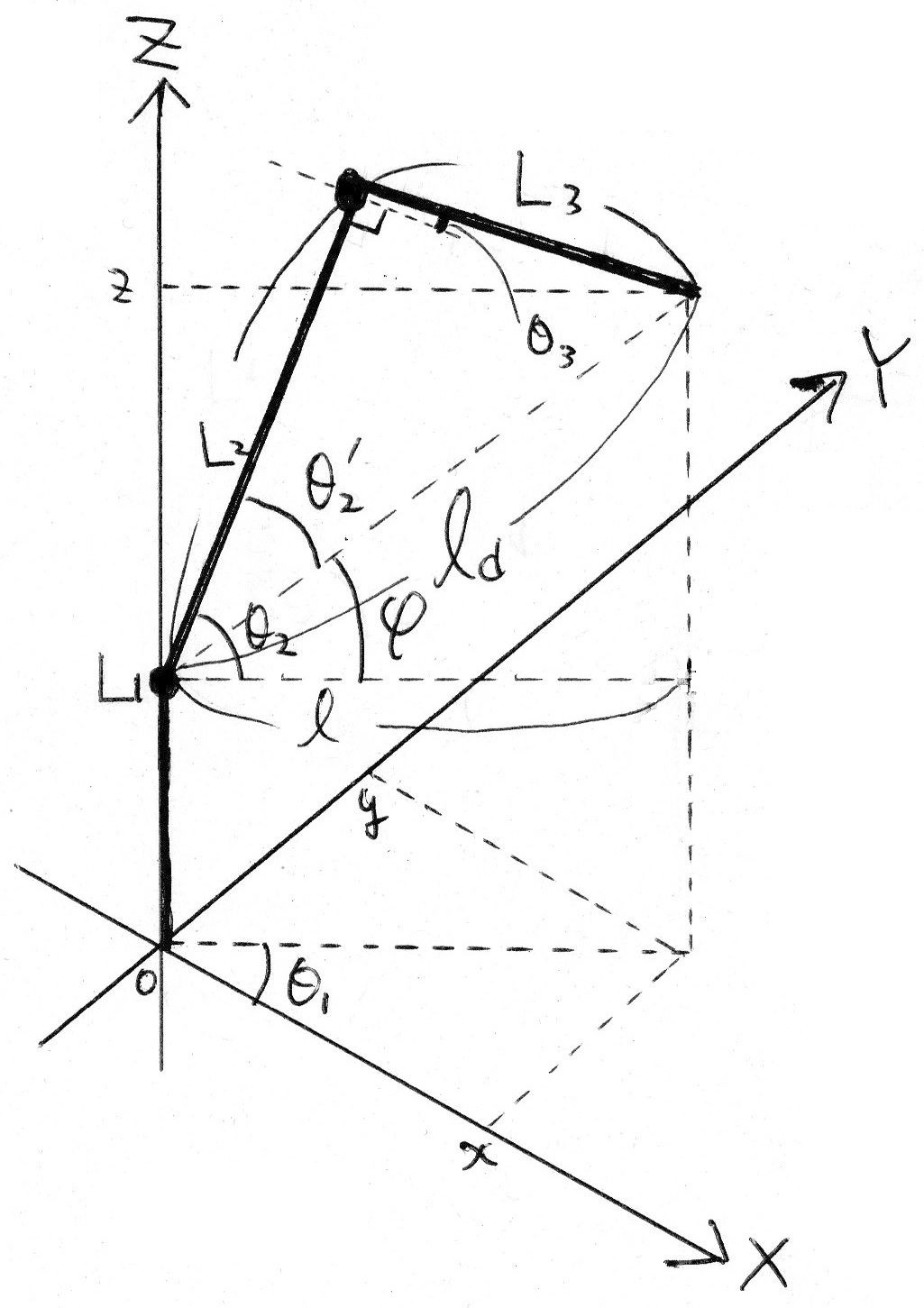
座標は以下のように平面上を(x, y)、高さをzとします。
首振りサーボの角度$θ_1$は平面座標(x, y)ですぐ導出できます。
$$θ_1 =\tan^{-1} \left(\frac{y}{x} \right)$$
2個目のサーボの角度$θ_2$は余弦定理を用いて導出します。
${L_3}^2 = {L_2}^2 + {l_d}^2 – 2{L_2}{l_d}\cos{θ_2}’$
${θ_2}’ = \cos^{-1} \left(\frac{{L_2}^2+{l_d}^2 – {L_3}^2}{2{L_2}{l_d}} \right)$
$$θ_2 = {θ_2}’ + φ = \cos^{-1} \left(\frac{{L_2}^2+{l_d}^2 – {L_3}^2}{2{L_2}{l_d}} \right) + φ$$
$$ 但し、φ = \tan^{-1} \left(\frac{z – L_1}{l} \right)$$
$$ l_d = \sqrt{l^2 + \left(z – L_1\right)^2}$$
$$ l = \sqrt{x^2 + y^2}$$
3個目のサーボの角度$θ_3$も余弦定理を用いて導出します。
${l_d}^2 = {L_2}^2 + {L_3}^2 – 2{L_2}{L_3}\cos \left(90°+ θ_3\right)= {L_2}^2 + {L_3}^2 + 2{L_2}{L_3}\sin {θ_3}$
$$θ_3 = \sin^{-1} \left(\frac{{l_d}^2-{L_2}^2 – {L_3}^2}{2{L_2}{L_3}} \right)$$
以上のとおり、所望の座標(x, y, z)とロボットアームの長さ$L_1$、$L_2$、$L_3$からサーボの角度を導出することができました。
参考
動作
逆運動学によって座標の指定のみでロボットアームの制御ができるようになったので以下のように線がひけます。
逆運動学を堪能
本当に座標通りに動いて ちょっと引いてるくらい#ロボットアーム pic.twitter.com/2wZIRCAtfR
— HomeMadeGarbage (@H0meMadeGarbage) December 7, 2019
Arduinoコード
冒頭に紹介した書籍の第5章サンプルコードを参考にプログラミングしました。
以下でArduinoサンプルコードをダウンロードできます。ありがたい!
https://www.ohmsha.co.jp/book/9784274222115/
求めた逆運動学の式を用いてロボットアーム先端の座標を制御します。
シリアルモニタで打ち込んだ文字によってロボットアームの動作を選択しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 |
#include <Servo.h> Servo myservo1, myservo2, myservo3; float th1=90,th2=90,th3=90; float phi,ld,l; int pos = 0; float L1=92,L2=137,L3=165; float x,y,z; void setup() { Serial.begin(115200); myservo1.attach(9, 500, 2420); //MG995 myservo2.attach(10, 820, 2140); //DS3115 myservo3.attach(11, 820, 2140); //DS3115 set_servo(); ik(-45, 228, 10); } void loop() { char c; if ( Serial.available() > 0 ) { c = Serial.read(); if(c=='1'){ //一を書く delay(100); for(x = -60; x <= 60; x += 5){ ik(x, 210, 0); delay(100); } ik(0, 170, 230); //初期姿勢 }else if(c=='u'){ //ウを書く ik(-45, 228, 10); delay(500); ik(-45, 228, 0); delay(200); ik(-45, 220, 0); delay(200); ik(-45, 220, 10); delay(200); ik(-57, 220, 10); delay(200); ik(-57, 220, 0); delay(200); ik(-54, 210, 0); delay(200); ik(-54, 210, 10); delay(200); ik(-57, 220, 10); delay(200); ik(-57, 220, 0); delay(200); ik(-35, 220, 0); delay(200); ik(-35, 210, 0); delay(200); ik(-37, 200, 0); delay(200); ik(-42, 195, 0); delay(200); ik(-42, 195, 10); delay(200); //ンを書く ik(-15, 220, 10); delay(500); ik(-15, 220, 0); delay(200); ik(-5, 210, 0); delay(200); ik(-5, 210, 10); delay(200); ik(15, 220, 10); delay(200); ik(15, 220, 0); delay(200); ik(10, 210, 0); delay(200); ik(10, 205, 0); delay(200); ik(8, 200, 0); delay(200); ik(-2, 195, 0); delay(200); ik(-10, 195, 0); delay(200); ik(-10, 195, 10); delay(200); //コを書く ik(35, 220, 10); delay(500); ik(35, 220, 0); delay(200); ik(60, 220, 0); delay(200); ik(60, 195, 0); delay(200); ik(35, 195, 0); delay(200); ik(35, 195, 10); }else if(c=='0'){ ik(0, 170, 230); //初期姿勢 } } } void ik(float x,float y,float z){ th1=atan2(y,x); l=sqrt(x*x + y*y); ld=sqrt(l*l + (z-L1)*(z-L1)); phi=atan2((z-L1),l); th2=phi + acos((ld*ld+L2*L2-L3*L3)/(2*ld*L2)); th3=asin((ld*ld-L2*L2-L3*L3)/(2*L2*L3)); th1=th1*180/3.14; th2=th2*180/3.14; th3=th3*180/3.14; set_servo(); } void set_servo(){ myservo1.write(th1); myservo2.write(th2); myservo3.write(th3); } |
おわりに
逆運動学によって座標の指定でロボットアームを自由に動かせるようになりました。
逆運動学 完全に理解した#ロボットアーム pic.twitter.com/gVv3euULnE
— HomeMadeGarbage (@H0meMadeGarbage) December 8, 2019
さて、次は現状ちょっと可動範囲が狭いのでアームの構成の調整と
もっと手軽にアームを制御できるように工夫したいと思います。
それではまた